第3章平面机构的运动分析

1．学习要求

1)了解进行机构运动分析的目的。

2）正确理解速度多边形及加速度多边形的概念和速度影像和加速度影像原理，并掌握其应用。

3）能用矢量方程图解法或解析法对I级机构进行运动分析，并掌握运用计算机进行机构运动分析的方法。

4）正确理解速度瞬心(包括绝对瞬心及相对瞬心)的概念，并能运用“三心定理”确定一般平面机构各瞬心的位置。

5）能用瞬心法对简单高、低副机构进行速度分析;对用综合法作复杂机构的速度分析方法有所了解。

6)了解速度图解在机械设计中的应用。

2．重点难点

本章的学习重点是对Ⅱ级机构进行运动分析。学习难点是对机构的加速度分析，特别是两构件重合点之间含有哥氏加速度时的加速度图解分析。

3．知识脉络

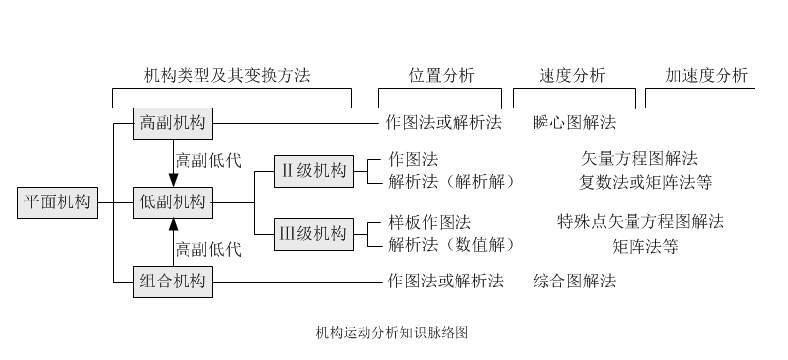
4.学习方法指导

(1）对机构运动分析一章学习的正确认识

首先，要认识到机构的运动分析的重要性。无论在设计新机械时，或是在利用现有机械时，或在作反求设计机械时，对机构进行运动分析都是十分重要的。在利用现有机械时，许多机械只有经过详细的运动分析，我们才能很好掌握它的性能，充分发挥机械的功能。如摇动筛机构（教材图3-8a)，只有知道了在一个周期中摇筛(构件4)的速度及加速度变化情况，才能知道它是否能达到很好的筛分效果。在反求设计中，常常只有经过运动分析后才能吃透原设计的意图，也才可能进行创造性的改进和发展。

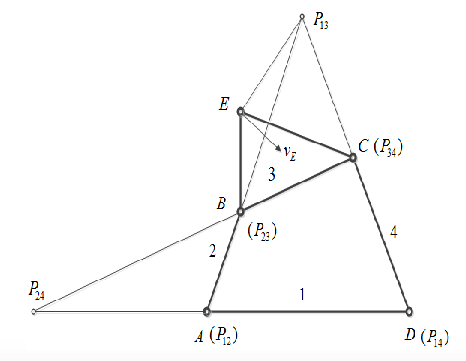
(2）在机构速度图解分析时要注意正确地应用速度影像关系

尽管机构中的每个构件均与其速度图有影像关系，但整个机构与其速度图无影像关系。故超出单个构件范围利用影像关系的作法是错误的。对加速度分析也一样。

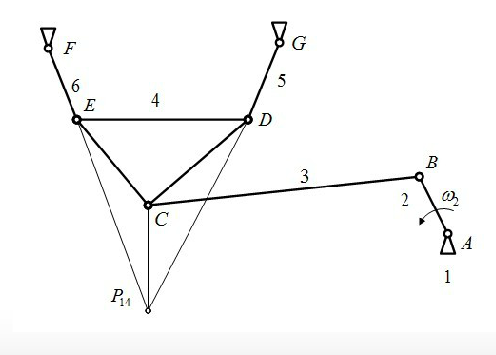
(3）正确掌握利用速度瞬心对机构进行速度分析的方法

首先，要认识到速度瞬心法是一种直观、快捷的速度图解法。利用速度瞬心对机构进行速度分析，其实质就是利用瞬心为两构件上的瞬时绝对速度相等的重合点（即同速点）这一概念。

其次，掌握这种方法的关键是要正确地找出所需瞬心的位置。即要找出待求运动构件与已知运动构件之间瞬心的位置。当这两构件直接组成运动副时，其间的瞬心位置很容易由瞬心定义直观地确定;当这两构件非直接接触时，其间的瞬心位置则可借助于三心定理来确定。为了便于确定机构中各瞬心的位置，可以利用瞬心多边形的帮助。

(4）用解析法作机构的运动分析时应注意的几个问题

1）关于用解析法作机构的运动分析时分析方法的选择问题。可用于机构运动分析的解析法非常多，但目前工程上较多采用的解析法主要有矢量方程解析法（即矢量分析法，详见第六版教材）、复数法和矩阵法。这些方法的区别在于:除了它们所采用的数学工具不同之外，在具体使用方便程度上也有一些差别。如用于Ⅱ级机构的运动分析时，直接用这三种方法均可获得求解，也比较容易。但如果是要获得所求运动参数的显式表达式的话，采用前两种方法显得更为方便。其中矢量法的概念较为直观、清晰，容易判断错误，但求解过程也较为繁琐，故一般多用于对新机构的分析;相比之下用复数法求解较为简单，其多于用对现有机构的分析。如果只要获得所求运动参数的数据结果，采用矩阵法最为方便，可借助于目前普遍使用的数学工具软件（如Matlab等）用计算机很方便地求解。当作IⅢ级以上机构的运动分析时，一般求解较困难。尤其是Ⅲ级以上机构，其机构的位置参数难以直接求得，需借助于数值法求解。用矩阵法较方便。

2）用解析法作机构的运动分析也有很强的程次性，要按着一定的步骤进行求解;而其求解的关键是要正确地作出机构的封闭矢量多边形，并写出相应的位置矢量方程式。其求解步骤如下:

首先建立一直角坐标系，并把各构件当作杆矢量对待。根据机构具有的独立封闭环数的多少，为每一独立封闭环各建立一矢量封闭方程。从只有两个未知量的矢量封闭方程开始求解，求解时可利用适当的矢量点积的方法消去一个未知量，从而求得另一未知量。在求得各杆矢未知量后，机构的速度和加速度分析只不过是位置方程对时间的一次求导和二次求导而已。这里还要说明两点:①用解析法作机构的运动分析时不需要准确作出机构运动简图，只要画出机构示意图即可;②各杆矢的方位角均应由轴开始，沿逆时针方向计量。作这样的规定，在书写方程和进行运算时具有统一的格式，给运算带来很大的方便。

5.典型案例

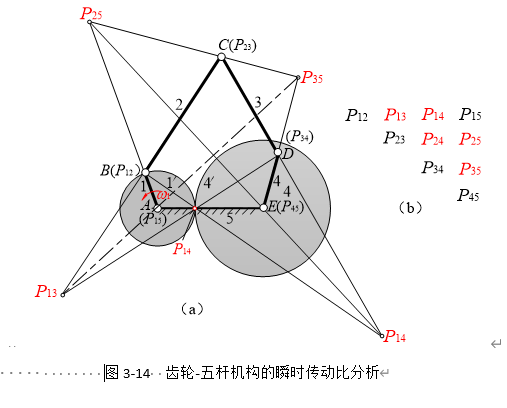
图3-14a所示为一齿轮-五杆机构，已知机构的尺寸和原动件1的角速度w1，逆时针方向转动，试求该机构在图示位置时全部瞬心位置和原动件1与各从动件2、3及4之间的瞬时传动比i₁₂、i₁₃及i₁₄。

解：由图a可知，该机构是由一对齿轮1′及4′组成的齿轮高副机构与铰链五杆机构ABCDE并联组成的组合机构，不难计算其机构自由度为1，因给定1个原动件1，故该机构运动是确定的。该机构的总瞬心数目K =N（N–1）/2 =5×(5–1)/2 =10，用列表法将这10个瞬心列出，如图b所示。其中瞬心P₁₂ 、P₂₃ 、P₃₄ 、P₄₅ 及P₁₅  由瞬心定义直观确定，P₁₄ 为构件1与4即两齿轮1′及4′高副处的相对瞬心，同时应位于其连心线P₁₅P₄₅上；而P₁₃ 、P₂₄ 、P₂₅ 及P₃₅ 则需要借助三心定理确定，如图a所示。

由图a可知，根据机构的传动比与相关瞬心的位置关系，瞬时传动比w1/w2、w1/w3 和w1/w4则分别由P₁₂与P₁₅及P₁₅、P₁₃与P₁₅及P₃₅和 P₁₄与P₁₅及P₄₅ 可求得，即

i₁₂= w1/w2 = P12P25/P12P15   （w2与w1方向相同）

i₁₃=w1/w3 = – P13P35/P13P15 （w3与w1方向相反）

i₁₄ =w1/w4 = P14P45/P14P15   （w4与w1方向相同）