第5章 机械的动力分析
第5章 机械的动力分析
1.学习要求
1)能正确理解机械效率,掌握机械效率用力或力矩计算机械效率和机组效率的方法,并了解提高机械效率的一些措施。
2)能正确理解机械自锁的概念和意义,掌握移动副及转动副的自锁条件和机械自锁条件确定的方法,了解自锁在机械中的一些应用。
2.重点难点
本章学习的重点是机械效率的计算,机械的自锁现象和自锁条件的确定。学习的难点是某些机械的自锁条件的确定。
3.知识脉络
4.学习方法
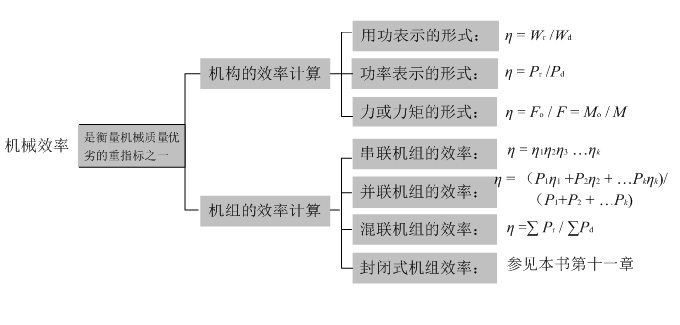
(1)用力或力矩表示的机械效率公式的意义
用功或功率之比表示的机械效率的计算是大家都比较熟悉的,用功之比(Wr, /Wa)表示的机械效率计算式一般需要已知力及其做功路程,故适合于效率的概念介绍和基本分析,而用功率之比表示的机械效率计算式则不仅需要已知力及其做功路程,而且需要做功所用的时间,因机器名牌上一般给出了机器的功率,故此式适合于机器效率计算。在此基础上本课又推导了以力或力矩之比的形式(Fo, /F或Mo/M)表达的效率计算式。此式对机构效率的计算具有普遍性、有效性和简便性。因为在计及摩擦的情况下,对机构进行受力分析可求得F或M,再令式中的摩擦因数及摩擦角为零,即可求得Fo或Mo,从而可求得机构的效率。
(2)用矢量方程图解法作机构的速度及加速度分析时应注意的几个问题
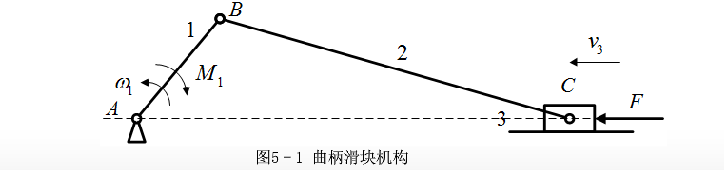
1)公式n=Fo/F=M/M中的Fo及F为驱动力,Mo及M为驱动力矩。而一个力或一个力矩是否为驱动力或驱动力矩,不是由我们主观假定的,而是看该力或力矩与构件之间的运动关系如何来确定的,如图5-1所示的曲柄滑块机构,设构件1沿逆时针方向回转,因M,与o方向相反,故为阻力矩,而F3与vs的方向一致,故Fs为驱动力。
2)在推导式n=Fo / F=Mo / M时,是根据克服同一生产阻力G的条件下,G/Fo=1 ,以及n=G╱F求得的,故要求Fo与F作用于同一点且方向不变,且对应于同一个阻抗力G;同样对于M与M则要求其作用在同一个构件上,且方向不变,并对应于同一个阻抗力G或阻抗力矩M’。至于机械效率的计算,一般很简单,并不难掌握,而由之出的结也很简单明确,但它们对我们设计机械却有重要的指导意义。
(3)正确理解机械的自锁的概念
机械的自锁是一个重要的概念,对机械的性能有重要影响。有时我们需要克服自锁,有时我们又需要利用自锁。因此必须正确理解什么是机械的自锁,所谓机械的自锁是指:自由度F≥1,从机构结构来讲原本可以运动的机械,在驱动力任意增大的情况下,都不能使之运动的现象。这里作一点补充说明,机械不能发生运动的可能原因有如下情况:
1)自由度F≤1,其结构本身就不能运动;
2)自由度F≥1,其结构本身是可以运动的,若机构不能运动又可能有如下情况:①机构的驱动力小于阻抗力,这时机构就暂时不能运动;②机构摩擦的存在原因,机构发生自锁而不能运动;③机构所处的位置原因,机构处于死点位置也会不能运动。
(4)注意掌握机械的自锁的判断方法
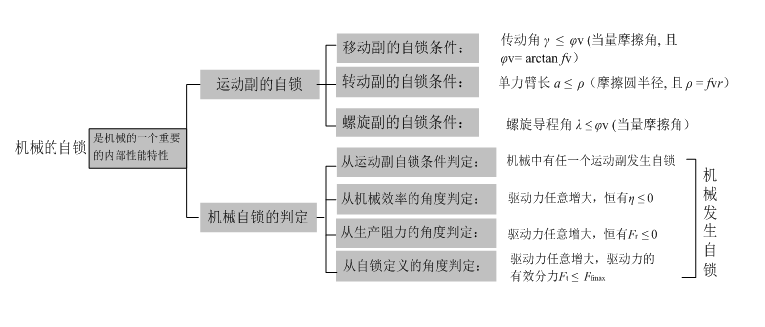
为了判断机械是否自锁和在什么条件下自锁,可根据已知条件和具体情况,采用下列方法之一来确定机械的白锁条件。
1)根据运动副的自锁条件来确定。其依据是机械发生自锁实质上是其运动副发生了自锁。换句话说,机械中有任一运动副发生自锁,它也就发生自锁。
①对于移动副,当驱动力作用在移动副的摩擦角之内时,将发生自锁。例如图5-2所示为一人在爬墙,当αi及α2均<qp时,人就可沿两墙之间上爬,而不致下滑。
②对于转动副,当驱动力为一单一力,并作用在摩擦圆之内时,将发生自锁。例如教材图5-9所示的偏心争夹具就是一个很好的例子。
③对于螺旋副,当螺纹导程角i≤pv将发生自锁。连接用螺纹的导程角.一般约为2.5°左右,而其当量摩擦角(~6°,故是自锁的。
2)根据生产阻力反号来确定。其依据是当驱动力任意增大时计算所得的机械的生产阻力均≤0 ,该机械发生自锁。因为这说明当驱动力任意增大时,机械都不能克服任何生产阻力而运动。
3)根据效率等于小于零的条件来确定。当驱动力任意增大时若机械的效率恒等于小于零(n≤0),机械发生自锁。其理由与上者所述相似。
4)根据自锁的概念来确定。根据作用在构件上的有效驱动力是否始终等于更所能引起的同方向上的最大摩擦力。

不自锁螺旋机构
(5)要注意机构自锁的方向性
在此必须指出,机构的自锁是有方向性的。所谓机构具有自锁性,是指机构以某一构件为主动件,在某些方向力的作用下不能运动,而不是说机构根本不能运动也就失去了作为机构的意义了。以后我们会讲到在蜗杆传动中,以蜗杆为主动件时,不会发生自锁;而以蜗轮为主动件时,则有可能发生自锁。
 螺旋千斤顶
螺旋千斤顶
5.案例分析
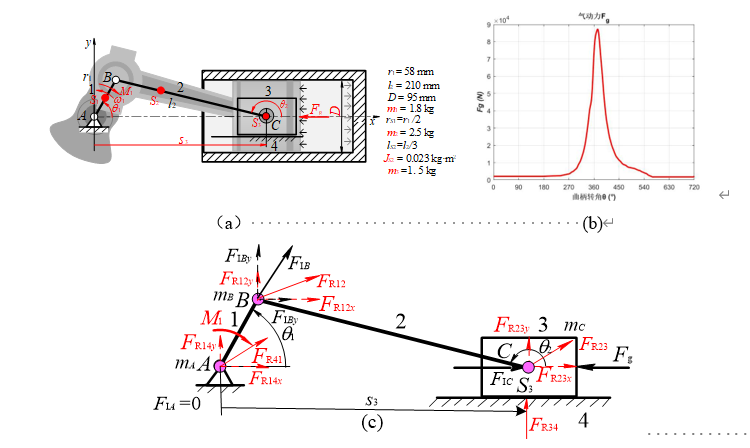
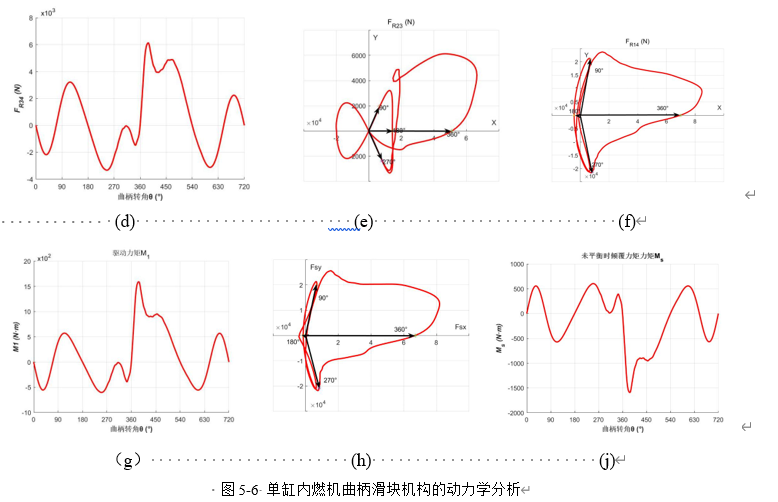
图5-6所示为一单缸四冲程内燃机曲柄滑块机构结构模型、实测各构件的质量等动力参数(图a)和活塞在一个工作循环中(q T =4p)所受气动力Fg (=pgπD2/4,其中pg为缸内气动压力,D为活塞直径)的变化情况(图b)。试分析该内燃机在一个工作循环内各运动副总反力和曲柄所需平衡力矩及其振动力等动力学行为。
解:1)确定机构各构件的惯性力 为方便求解,由于质量静代换一般可以较好满足工程的动力分析精度要求,故选取连杆上点B和C为静代换点对其m2进行质量静代换,则有mB2=2m2/3= 1.67 kg,mC2=m2 /3= 0.83 kg;并选取曲柄上A和B为其质量m1的两静代换点,则mA1= mB1=m1/2=0.9 kg。于是该机构各构件的质量重新分布于三个铰链中心A、B、C处,即mA= mA1、mB= mB1+ mB2及mC = m3+ mC2。因A点无加速度,B点仅有法向加速度aB = –rw21,而滑块C的加速度aC(= a3),由式(5-13c)或式(5–13c')确定,故该机构仅在B、C两点处有惯性力,即
FIB = – anBmB = – anBxmB – i anBymB = r1w21mBcosq1 + i r1w21mBsinq1
FIC = – aCmC = – a3 mC = r1w21 mC[cosq1 + (r1/l2)cos2q1]
2)确定各运动副总反力 因不考虑摩擦力和重力,故该机构的连杆2为二力杆,则FR32 = – FR12,而其他运动副总反力:FR34= –FR43,FR23= –FR32 = FR23x+ iFR23y,FR12= – FR21= FR12x + iFR12y,FR14= –FR41= FR14x+ iFR14y,建立其动力学模型,并示出其气动力、各惯性力及各运动副总反力的方向及其分量,如图c所示。
取连杆2与滑块3的杆组为分离体,受有力FR12、FIC、Fg及–FR34,故根据 MB=0,即其外力Fg、FIC及–FR34对B点取矩,可得
(FIC –Fg)lsin(180 – θ2)+ FR34lcos(180 – θ2) = 0
由此可得
FR34= –FR43= i (FIC – Fg)tanθ2 = – i (a3mC + Fg) tanθ2
其中tanθ2= (r1/l2)sinq1/{ 1–[(r1/l2)sinq1]2}1/2 。
取滑块3为分离体,其受有力FR23、Fg、FIC和–FR34,故由 F= 0,即FR23– Fg+ FIC – FR34 =0,由此可得
FR23= –FR32 = Fg – FIC + FR34
即 FR23x + i FR23y = Fg + a3mC – i(Fg+ a3mC )tanθ2
因FR12 = –FR32= FR23,故有FR12 = –FR21 = FR12x + iFR12y = FR23x + i FR23y。
取曲柄1为分离体,受有力–FR12、FIB及–FR14和平衡力矩M1,由F= 0,即–FR12+FIB –FR14=0,可求得
FR14 = –FR41 = –FR12+ FIB
即 FR14 = –FR41 =FR14x+ iFR14y = (FR12x + FIBx) + i(FR12y + FIBy)
= Fg + a3 mC + r1w21mBcosq1+ i [ (r1w21mBsinq1Fg – a3 mC )tanθ2 ]
3) 确定曲柄的平衡力矩M1 对曲柄1取MA= 0,即外力–FR12及FIB对A点取矩,可求得
M1 = – (FR12x +FIBx)r sinq1 – (FR12y+ FIBy)rcosq1
= – ( Fg + a3mC + r1w21mBcosq1)r1sinq1 – i[(Fg+ a3mC ) tanj2+ r1w21mBsinq1] r1cosq1
4)确定振动力Fs和振动力矩Ms 对于该单缸内燃机来说,只有通过铰链A和滑块3导路会产生振动力和振动力矩,则
Fs = FR14+ FR34 = – (Fg + a3 mC) + r1w21mBcosq1+ i r1w21mBsinq1
Ms = – MA= s3FR43= –s3FR34= sC(Fg+ a3mC) tanθ2
由此可见,内燃机的振动力和振动力矩仅与气动力和惯性力矩有关,其中惯性力矩是w21的函数,故该振动力Fs对内燃机的速度变化十分敏感。
据上述关系式,进行编程计算,并绘出当w1=3400r/min时在一个循环周期内,该内燃机的各运动副总反力线图(图d 副)、曲柄1所需的平衡力矩线图(图g)以及作用于机架上振动力Fs(图h)和振动力矩MS线图(图j)。