第7章 运转与调速

1.学习指导

1)了解机械运转过程三个阶段的速度及功能特征和常见实际驱动力和工作阻力的机械特性;

2)正确理解机械系统等效动力学模型及其等效转动惯量（或等效质量）和等效力矩(或等效力）的概念及等效条件，掌握建立单自由度机械系统的等效动力学模型和运动方程的方法，能求解运动方程式。

3）了解机械周期性速度产生的条件和程度表示，掌握周期性速度波动与机械非周期性速度波动调节的基本原理和方法。

4）了解飞轮调速原理,掌握飞轮转动惯量的简易计算法。5)对考虑构件弹性时的机械动力学有所了解。

2.学习重点

本章的学习重点是:

1）关于等效力矩（或等效力）和等效转动惯量（或等效质量）的概念及其计算方法;单自由度机械系统的等效动力学模型的建立。

2）机械运转产生周期性和非周期性速度波动的根本原因及其调节的基本原理和方法，机械系统周期性速度波动调节时飞轮转动惯量的简易计算。

本章的学习难点是:

1）根据不同特性的机械系统等效动力学模型对应的机械运动方程的求解。

2）计算飞轮转动惯量时最大盈亏功的确定。

3.知识脉络

4.学习方法

(1）明确机器动力学研究的主要基本问题。机器动力学研究的主要内容是两类基本问题:

其一是分析机器在运转过程中其各构件的受力情况，以及这些力的作功情况，教材第四、五两章介绍的内容就是这方面的问题;

其二是研究机器在已知外力作用下的真实运动，这是本章将要研究的主要问题之一。

机器的真实运动规律是由其各构件的尺寸、质量、转动惯量和作用在各构件上的力等诸多因素决定的。由于这些因素的变动，机械运动速度一般是波动的，这种速度波动将直接影响到机械的工作，所以必须设法加以调节，使其速度波动控制在许可的范围之内，这就是调速问题。这是本章将要研究的另一主要问题。

(2）搞清机械真实运动求解及其动力学模型建立。

一般机械的自由度为1，对于自由度为1的机械，只要能确定其某一构件的真实运动规律，其余构件的运动规律也就相应确定了。因此，在我们研究机械的运转情况时，可把机械系统简化为对机械中某一选定的构件来进行研究，但为了保持机械原有的运动状态，要把其余所有构件的质量、转动惯量都等效转化（即折算）到这个选定的构件上，并把各构件上所作用的力、力矩也都等效转化到这个构件然后列出此构件的运动方程式，研究其运动规律。这一过程，就是建立等效动力学模型。显然，这里关于质量、转动惯量、力及力矩的等效转化的概念是非常重要的。所以必须把质量、转动惯量、力及力矩等效转化的条件和方法搞清楚。

(3）机构各构件的质量和转动惯量虽然一般都是定值，但转化后的等效转动惯量，因和各构件与转化构件的传动比有关，所以除非这些传动比均为定值，否则等效质量及等效转动惯量都是机构位置的函数。

(4）机械的等速运转只有在等效驱动力矩和等效阻抗力矩随时相等（亦即驱动功率和阻抗功率随时相等）的情况下才能实现。否则，机械运转的速度将发生波动，而机械运转速度的波动有两种不同的形态。一种是周期性的速度波动。产生这种速度波动的条件是:在一个运动周期内机械的等效驱动力矩和等效阻抗力矩的平均值是相等的(亦即其驱动功和阻抗功是相等的)，所以机械处于变速稳定运转状态。另一种则是非周期性速度波动。这时机械的驱动功和阻抗功已失去平衡，机械已不再是稳定运转，机械运转的速度将持续升高或持续下降，如不加以调节就不可能恢复到稳定运转状态。机械的周期性速度波动和非周期性速度波动是两种性质完全不同的现象。学习时必须把它们发生的原因、速度波动的形态以及调节的方法分别搞清，不要混淆。

(5）周期性速度波动可用飞轮进行调节，而非周期性速度波动则通过调速器来调节。飞轮的作用是当机器出现盈功时用动能的形式把多余的能量吸收和储存起来，当机器出现亏功时又把储存的能量释放出来以弥补能量之不足，从而降低机器运转速度的波动程度，即在机器内部起转化和调节功能作用，而其本身并不能产生新的能量。调速器的作用则不同，它是从机器的外部来调节输入（或输出）机器的能量，使机器恢复稳定运转。两者的调速原理不同，解决的问题也不同。正因如此，所以在同一部机器中可能既装有飞轮又装有调速器，这也是一个必须搞清楚的概念。

砂轮磨削平面

(6）飞轮实质上是一个能量储存器，飞轮储能具有容量大、寿命长、无污染等特点，目前对其研究在不断深入。复合材料是制造储能飞轮的最好材料，近年来由于高强度碳素纤维的出现，飞轮允许的线速度达500m/s~1000m/s，增加了飞轮单位质量的动能储量，使得储能飞轮的应用领域不断发展。如飞轮电池主要可用于电动汽车上，在军事上可用于战斗车辆、电磁炮等。电磁炮是利用电磁发射技术制成的一种先进武器。它是利用电磁场的作用力代替火药爆炸力来加速弹丸的发射系统，因电磁力作用时间长，可大大提高弹丸的发射速度和射程。电磁炮最大的缺点是消耗功率大，若以3km/s的速度发射1.Okg重的弹丸，需要200万千瓦以上的功率。因此电磁炮研究中的一项重要工作就是寻找储存操作电磁炮所需的庞大电量，用复合材料制成的飞轮取代庞大的电容器可使大炮体积大为减小。高速旋转的飞轮可贮存庞大的能量，当大炮发射时，飞轮四周的磁线圈把旋转的动能瞬间转变为大电流。目前研制的电磁炮已能将弹丸加速到8~10km/s（普通大炮仅为2km/s)，预计将来电磁炮弹丸的速度可达100km/s 。

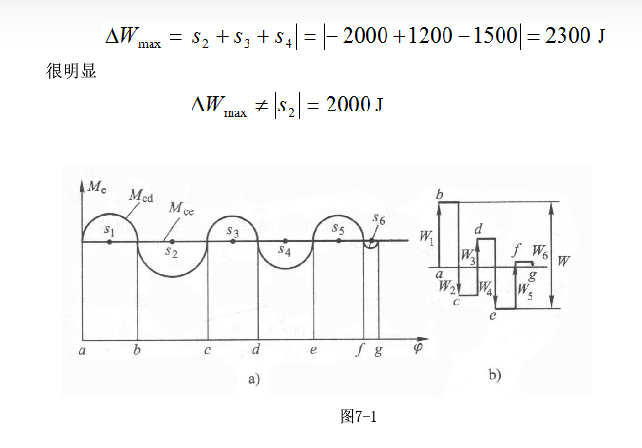
(8）计算飞轮转动惯量的关键是确定该机械系统的最大盈亏功，而为了确定最大盈亏功，需先确定机械最大动能及最小动能出现的位置。对于一些比较简单的情况，最大动能及最小动能出现的位置可直接由图中看出;对于复杂的情况，则可借助于教材中介绍的“能量指示图”来确定。值得注意的是，不要简单地以为在图中，Ma与M之间所包围的诸面积之中，面积最大的一块面积之值就代表最大盈亏功的大小。例如图7-1a所示为某一机械在一个运动循环中的等效驱动力矩M和等效阻抗力矩Me的变化曲线。设两曲线间包围的各小块面积所代表的盈亏功分别为s1 =1400 J,s2 =-2000 J,.S3=1200 J，s4 = -1500 J,s5 =1000 J,s6= -100 J。要确定其最大盈亏功，要先画出其能量指示图(图b)。由图中可看出在点b处动能最大，在点e处动能最小，点b、e间的各块盈、亏功的代数和的绝对值即为最大盈亏功。

(9）考虑构件弹性时的机械动力学部分是属于扩展知识面性质的内容，随着机械日益向高速、高精度、轻巧方向发展，其重要性也日益显露出来。但因此方面的内容涉及较深的数学及振动方面的知识，故教材中只作了非常肤浅的简介，若有需要可参考专门的文献。

5.案例分析

 结合图6-17所示为一单缸四冲程内燃机曲柄滑块机构结构及机构动力学模型，此时系统等效质量为m_B= m_B1+ m_B2及m_C = m₃+ m_C2和平衡质量为m_B'=m'+m''。现要求对该内燃机平衡后在活塞气动驱动力F_g（其机械特特如图5-20b所示）和要求曲轴输出克服平均负载特性（即其阻抗力矩Mr为常数）下其曲轴的真实运动求解和速度波动特性分析，并要求其运转速度不均匀系数δ<[d]=0.05，否则需加以调节。

   解：1) 曲柄（曲轴）1输出生产阻力矩M_r1的求解  由于单缸内燃机的运转属于变速稳定运转，故在不考虑摩擦损失时，在一个工作循环周期内，活塞气动驱动力Fg之功应等于曲轴输出能克服的平均生产阻力矩M_r1（常数）的之功，即W_r = 4πM_r1 =W_d(Fg)。因Fg等效于曲柄1上的等效驱动力矩如图5-20b所示曲线，其功需利用数值积分计算，故由MATLBA通过积分求平均值，可得M_r1=130 N·m。

2）单缸内燃机的曲柄1真实运动方程建立  由于该单缸内燃机的活塞气动驱动力和等效转动惯量均为周期为q_T = 4p的周期性的函数，而曲轴（曲柄）输出为平均负载特性即为常数。为了了解该内燃机的速度周期性变化特性，现需建立其运动方程式，为此，取曲轴（曲柄）1为等效构件，建立其等效动力学模型。

由于等效力矩和等效转动惯量的确定与机构的传动比有关。由式（3-30b）活塞的速度线图（图3-17c）分析可知，其速度主要呈现出基本波动的正弦波形，表明其二阶谐波项(0.5r₁/l)sin2q₁ 对其速度变化影响很小，加之高阶项将对其运动建模及求解极大困难，故其可以忽略不计而并不影响其分析精度要求。于是有v_C =v₃ ≈ – r₁w₁sinq₁，即v₃/w₁≈– r₁sinq₁。故该等效构件曲柄1的等效力矩M_e1为

M_e1 = M_de –M_re = –F_g(v₃ /w₁) –M_r1 = F_g r₁sinq₁–130 N·m  

而因该内燃机系统平衡后的等效质量有m_B、m_C、m_B'，故其等效构件曲柄1的等效转动惯量为

J_e1 = m_B r₁² + m_B' r'^'2 + m_C(v₃/w₁)² = r₁²m_B  + m_B' r^'2 + r₁²m_C sin²q₁

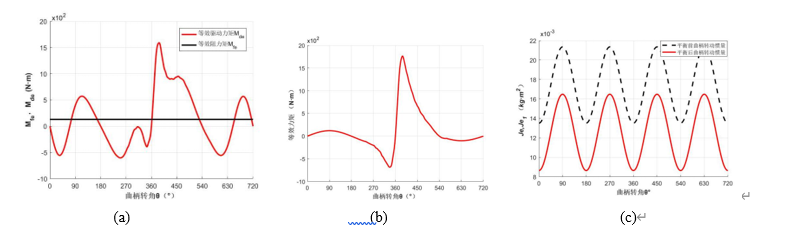
由此计算可得，等效力矩M_e1和等效转动惯量J_e1的一个周期变化特性曲线分别如图7-11a及b所示。

    由此可见，该机械系统的等效转动惯量和等效力矩均为机构位置和速度的函数，故其动力学运动方程需采用微分形式，即                

         d[ (r₁²m_B + m_B' r'^'2+ m_C r²sin²q₁) w₁²/2] = (F_gr₁sinq₁– M₁)dq₁

即                 (r₁²w₁²m_Csin2q₁ /2)dq₁ + w₁ (m_B r₁²+ m_B' r^'2+ m_C r₁² sin²q₁) dw₁= (F_g r₁sinq₁– M₁)dq₁

    3）单缸内燃机的曲轴真实运动求解  由于上式是一个非线性微分方程，故需采用差分法进行数值求解。故当q₁=q_1i时，则w₁=w_1i，此式中dq ₁ 用Dq₁ 近似代替，即Dq₁= q_1i+1–q_1i；dw₁用Dw₁ 代替，即 Dw₁ = w_1i+1– w_1i。由此可得

[r₁²w_1i ²m_Csin2q₁ /2] Dq₁ + w_1i (m_B r₁² + m_B' r^'2 +m_C r₁²sin²q₁) (w_1i+1–w_1i) = (F_g r₁sinq₁– M₁) Dq₁

w_1i+1 = w_1i + (F_g r₁sinq₁– M₁ –r₁²w_1i ²m_Csin2q₁ )Dq₁/[ r₁²w_1i (m_B + m_B' r^'2 +m_C sin²q₁)]

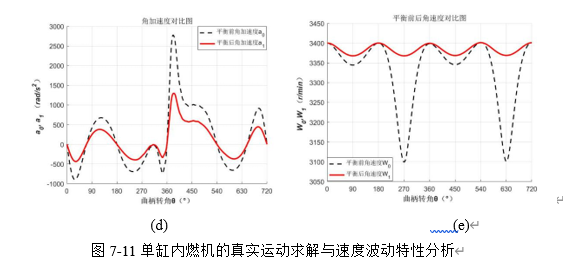
据此，进行编程并利用MATLBA计算，基于F_g的特性曲线，可得在一个循环周期4p内曲柄1在真实外力作用下的真实运动的角加速度α₁和角速度变化ω₁曲线如图7-11d及e所示。