实验5.3 单透镜望远镜
单透镜望远镜
(点击查看PPT)
一、实验目的
1.学会制作简易的单透镜望远镜;
2.定性测量小孔孔径与成像之间的关系;
3.掌握测量单透镜望远镜视角放大率的方法。
二、实验器材
凸透镜(1块),PVC 管(2个,两管可以嵌套),不透光圆片,穿孔器具等
三、实验原理
自1608年荷兰的眼镜商汉斯•利伯希发明第一块望远镜以来,望远镜在天文观测、军事观察以及日常娱乐生活中发挥了重要的作用。按望远镜的组成结构来分,可分为开普勒望远镜和伽利略望远镜。在日常生活中,使用最广泛的是开普勒望远镜。它由两块凸透镜组成:一块用作物镜,成倒立、缩小的实像;另一块用作目镜,使物镜所成缩小的实像被放大成正立的虚像。根据小孔成像原理,可以使用小孔代替目镜放大透镜成的像,从而组成一个单透镜望远镜。单透镜望远镜光路如图1所示。
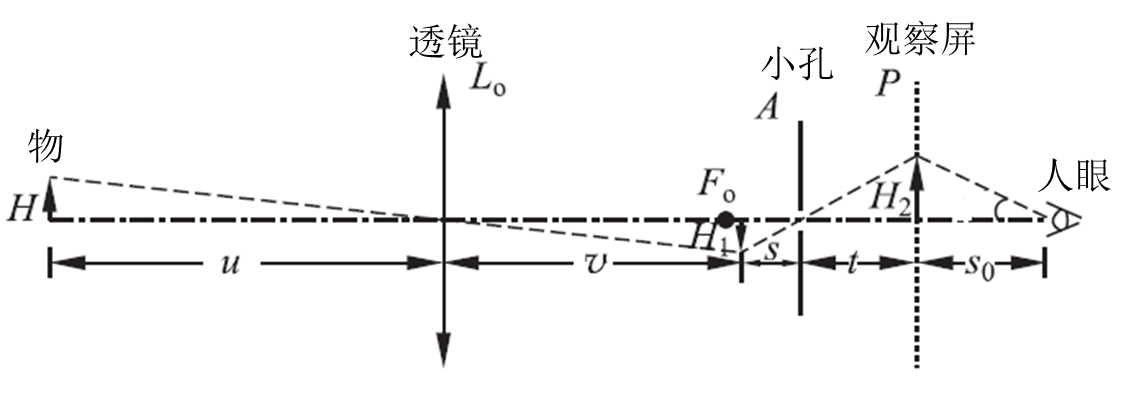
图1 单透镜望远镜光路图
其中:Fo 是透镜焦距,s 和 t 分别为小孔成像的物镜与像距。
1.视角放大率的测量
视角放大率是望远镜一个重要的参量,表征望远镜的放大能力。望远镜的视角放大率是指像对人眼的张角与物对人眼张角的比值。对单透镜望远镜而言,如果光线满足近轴条件,物体到透镜的距离远大于透镜的焦距,人眼靠近屏幕观察,则视角放大率满足以下公式:
M = ft / ss0(1)
其中,f 是透镜焦距,t 为观察屏到小孔的距离,s 为透镜所成像到小孔距离,s0为人眼到观察屏的距离。
2.分辨率
当像平面上的上的两个光斑恰好没有重叠即相切时,可以视为能够分辨,即清晰。设物平面上的两点相距为ΔH ,若使像平面上的两个光斑恰好没有重叠,则需满足下式:
ΔH =ud(s + t)/vt (2)
其中,d 为小孔直径,其余参量见图1。由此可知,不考虑衍射的情况下,分辨率与小孔直径成正比,而与小孔到屏幕的距离成负相关关系。如考虑到衍射效应,由衍射理论可知,通常情况下透镜的衍射效应可以忽略。而对小孔衍射效应,若小孔尺寸较大,其衍射效应可忽略;若小孔尺寸较小时,需考虑小孔的衍射效应,此时像的清晰度是几何光学和衍射效应的综合。
四、实验内容(点击查看实验视频)
1.定性观测小孔直径与像清晰度的关系
 图2 单透镜望远镜装置示意图
图2 单透镜望远镜装置示意图
按照图2所示,自制实验设备。
(1)小孔圆片的制作:使用不透光的薄片,按照套筒大小剪成圆片,在中心处打圆孔;制作10个小孔圆片,孔径分别为0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm、3 mm、3.5 mm、4 mm、4.5 mm和5 mm。
(2)套筒的制作:使用两个直径不同、不透光的圆筒,透镜置于大筒的一端。
使用平行光法测量透镜的焦距;小孔圆片置于小筒一端,使用黑色胶带缠绕小筒(缠绕的圈数以实际情况而定),使小筒伸入大筒,仔细调整,使小筒可在大筒中自由伸缩。
(3)清晰度测试:首先用平行光法测量透镜的焦距;然后,选择孔径为0.5 mm圆片置于小筒一端;把观察屏置于小筒前方,调节观察高度,使观察屏中心与套筒中心的高度大致相等;伸缩小筒,仔细调节小孔圆片的位置,并调节观察屏的位置使观测到像最清晰,拍摄观察到像。最后依次选用其他孔径圆片,重复步骤(3),记录数据。
2.视角放大率的测量
(1)选择孔径为1.0 mm的小孔圆片,按图二安置光路,记录透镜 L0 的位置;
(2)调节小孔圆片位置及观察屏位置,使观察屏上的像最清晰,记录小孔圆片与观察屏的位置,分别为 A、P;
(3)取下观察屏,眼睛沿着套筒轴线前后观察像,使观察到的像最清晰,记录眼睛所在的位置E;
(4)重复测量三次,取每个变量的平均值代入公式(1)得到单透镜望远镜的视角放大率;
五、数据处理
1.观察小孔孔径与成像清晰度的关系,使用手机拍摄单透镜望远镜观察到的照片,并记录小孔孔径大小。
2.视角放大率的测量,自拟表格,计算测量得到的视角放大率。
注意事项
1.小孔圆片是不透光材料;
2.套筒长度应该与透镜焦距匹配,即不能比焦距长很多;
3.尽量保证大小筒共轴,且使小孔中心与套筒中心轴大致等高。
六、思考题
1.分析单透镜望远镜的误差来源。
2.简述小孔在单透镜望远镜中的作用。
七、参考文献
1.潘开欣,刘怡然,潘志民. 单透镜望远镜及其成像参数的研究[J].物理与工程,2017, 27(6):116-122.
2.向柳嫒,杨运珊,王俊豪,黄敏. 小孔成像的清晰度分析及其在单透镜望远镜中的应用[J]. 物理通报,2018, 10:121-124.
八、自测题
说明:自测题需用微信打开链接进行自测。若加载有问题,可点击链接进行自测。